>> CHIPTUNING  ALGEMEEN  >>  KOPPEL & VERMOGEN

Deze fysische grootheden zijn vaak de beslissende parameter bij de aankoop van een wagen.
De samenhang tussen deze parameters is vrij eenvoudig :

P = M x ω  waarbij P = vermogen in W (Watt) | M = draaimoment in Nm | ω = hoeksnelheid in rad/s.

Het mechanisch vermogen P is een fysische grootheid die aangeeft hoeveel arbeid W in een bepaalde
tijd Δt verricht wordt, of beter hoeveel energie in deze tijd wordt omgezet. Vermogen is dus het
quotiënt uit de overgedragen energie, of de verrichtte arbeid in een bepaalde tijd.
 

P =

ΔW   Δt

waarbij P = vermogen in J/s of W (Joule per seconde of Watt). Vaak wordt het vermogen uitgedrukt in PK. Hierbij geldt dat 1 kW = 1.36 PK of 1 PK = 0.7355 kW

De fysische grootheid arbeid W is het produkt uit de kracht F en de afgelegde weg Δs.
 

ΔW = F x Δs

omdat snelheid v de afgelegde weg per tijd is krijgen we een nieuw produkt

P =

F x Δs     Δt

= F x v

Hierdoor kunnen we zeggen dat vermogen de werking van een kracht bij een bepaalde snelheid uitdrukt.

Het draaimoment M is een fysische grootheid die bij een rotatie of draaibeweging van lichamen optreedt.
Deze draaimomenten spelen dezelfde rol als krachten bij een translatie of rechtlijnige bewegingen.
Bij een rechtlijnige beweging grijpt een kracht, om een versnelling te bekomen, aan het zwaartepunt van
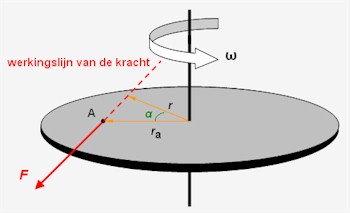
het lichaam, zelf in. Bij een rotatie dewelke om een vaste as plaatsvindt, werkt de kracht langs een
werkingslijn, die buiten de as in afstand r van deze as ligt.
 

Praktisch gezien kan men zich dit voorstellen als volgt. Veronderstel een denkbeeldige draaibare as,
bv krukas, waaraan een 1 meter lange hevel is bevestigd. De beschikbare kracht aan het einde van deze
hevel, dus 1 meter vanaf het middelpunt van de krukas, is het zogenaamde draaimoment.
Volgens het hefboomprincipe is het draaimoment afhankelijk van de kracht F en de loodrechte afstand r
tussen de werkingslijn van de kracht F en de draaias.
 

M = F x r  of beter voor een afstand ra dewelke een hoek α maakt met de loodrechte afstand r geldt : M = F x ra x cos α  waarbij de eenheid voor draaimoment in Nm wordt uitgedrukt (Newtonmeter).

Het vermogen en het draaimoment of koppel zijn karakteristieke waarden voor een motor.
De manier waarop deze waarden ontstaan in een standaard motor wordt hieronder beschreven.

Een viertaktmotor is een zuigermotor die twee complete omwentelingen maakt om weer in de uitgangstoestand terug te keren. De motor is uitgevonden door Nicolaus Otto in 1876 en wordt daarom
soms ook wel Ottomotor genoemd.
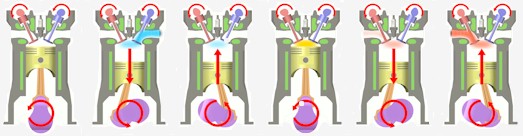
Startend met een lege cylinder met de zuiger in de bovenste positie zijn de vier slagen :

• inlaatslag : een inlaatklep gaat open en de zuiger gaat naar beneden, brandbaar gasmengsel
  vult de cylinder.

• compressieslag : de klep gaat dicht en de zuiger gaat weer naar boven.

• arbeidsslag : een vonk (bij benzinemotoren) of de warmte van de compressie (bij dieselmotoren) ontsteekt het mengsel en de zuiger wordt door de explosie met kracht naar beneden geduwd.

• uitlaatslag : een uitlaatklep gaat open, en de zuiger gaat naar boven en drukt het afgewerkte gasmengsel uit de cilinder.

De viertaktmotor is een warmtekracht-machine met inwendige verbranding waarbij chemische energie in
warmte-energie en vervolgens in mechanische arbeid wordt omgezet.
Voor verbranding van brandstof is zuurstof nodig die met de lucht wordt aangevoerd. Deze lucht dient
terzelfdertijd als arbeidsmedium, dat door warmtetoevoer onder druk gezet wordt en bij expansie arbeid
verricht. De zuiger beweegt door de druk naar onder en er begint een periodische voortgang, gekend als
een thermodynamisch proces. Tijdens deze voortgang wordt brandstof en lucht aangevoerd en de verbrande
gassen afgevoerd. Om deze ladingswissel of gaswissel door te voeren zijn er 4 arbeidstakten nodig.

De belangrijkste takt is de arbeidsslag. De drukkracht F die ontstaat door de expansie bij de verbranding
wordt via de zuiger en de zuigerstang op de krukas overgedragen. De bewegingsenergie van de zuiger
wordt omgezet in een draaibeweging van de krukas. Zowel in de cylinder als aan de krukas wordt een
kracht in een bepaalde tijd verricht. Per definitie is dit dus vermogen dat op verschillende plaatsen vrijkomt.
Dit vermogen, dat op de cylinder tijdens de gasexpansie ontstaat, wordt inwendig vermogen genoemd Pi.
Het vermogen aan de krukas, of het vliegwiel, wordt effectief vermogen Peff genoemd. Dit vermogen dat
ontstaat uit Pi  en na aftrek van alle wrijvingsverliezen, is het eigenlijke vermogen van een motor dat op een proefstand gemeten wordt. Het inwendig vermogen daarentegen is het theoretische, door de binnendruk opgebouwde, vermogen. Dit vermogen kan niet gemeten worden maar wordt berekend.
In de auto-industrie wordt het vermogen van een motor onder bepaalde voorwaarden bepaald (DIN-norm),
De "norm-toestand" is Tu = 298 K, Pu = 1 bar en 30 % relatieve luchtvochtigheid. De betrekking op een
vastgestelde omgevingstoestand is belangrijk omdat het motorvermogen bij verschillende luchttoestanden
verandert. Ze neemt toe bij zware lucht. Bij 100 meter hoogtetoename daalt het vermogen met 1%.
Ook vochtige lucht vermindert het motorvermogen.

Om de berekening van het vermogen en de relatie tot het koppel vast te stellen wordt verder het ontstaan
van van het draaikoppel verklaart.
Uit de lineaire beweging van de zuiger resulteert bij de verbranding van het brandstof-luchtmengsel een gaskracht. Bovendien werken in complete drijfwerk krachten, die ten gevolge van massa versnellingen
optreden en daarom massakrachten worden genoemd. Ten gevolge van het cyclische arbeidsproces en het
niet gelijkvormige bewegingsverloop onstaan er uit de gaskrachten en de massakrachten talrijke varierende
"inwendige" en "uitwendige" krachten. De inwendige krachten zijn voor de zuiger, drijfstang, krukas en
lagers bestemt terwijl de vrije uitwendige krachten oorzaak zijn van krachten en momenten van de motor
die zich vertalen in trillingen en in de motorlagers opgenomen moeten worden.

Eenheden, berekeningen en ontstaan van massakrachten zijn niet hier niet noodzakelijk voor de verdere
uiteenzetting. Belangrijk is wel te weten dat massakrachten tot sterke wisselkrachten voeren en de motor
vooral bij hoge toerentallen beduidend beïnvloeden. Massakrachten stijgen lineair met de massa en hebben
tot doel om bij een motorconstructie lichte zuigers, zuigerpennen en drijfstangen aan te wenden.
Bij lage toerentallen zijn de voornaamste krachten het resultaat van gaskrachten dewelke door de
cylinderdruk aan de zuiger wordt doorgegeven. Neemt men de periodisch werkende gaskracht en de
periodisch werkende massakracht van het drijfwerk tesamen, houdt men de resulterende
zuigerkracht Fz over.

Welk draaimoment of koppel ontstaat nu uit het verloop van deze resulterende zuigerkracht,
oftewel het verloop van de dominerende gaskracht in de arbeidscylinder ?
Dit is afhankelijk van de geometrie van krukas en de drijfstang.
 

De zuigerkracht Fz laat zich splitsen in een drijfstangkracht Fz en een normaalkracht Fn. Deze Fn is de kracht waarbij zich de zuiger tegen de cylinderwand afstoot en Fz de kracht die langs de drijfstang werkt en aan de krukas aankomt. Deze kracht laat zich weerom splitsen in een tangentiaalkracht Ft en een radiaalkracht Fr Deze radiaalkracht belast de krukas en de lagers en draagt geenzins bij tot het draaimoment omdat de lastarm nul is. Eenvoudiger verklaart is dat deze radiaalkracht ervoor zorgt dat de krukas niet naar beneden "valt" als de drijfstang zich "afstoot" op deze. Het draaimoment van een motor hangt volledig af van enkel de tangentiaalkracht Ft . Het draaimoment staat in een vaste verhouding tot deze kracht omdat de krukasradius r, eenmaal vastgelegd bij de constructie, een constante is. M = Ft x r

Het draaimoment van de krukas ontstaat door de aan de krukpin aangrijpende tangentiaalkracht Ft die enkel
een gedeelte van de zuigerkracht Fz vertegenwoordigd zodat we de tangentiaalkracht kunnen uitdrukken als
Ft = c x Fz waarin c een factor is die zich laat berekenen uit de krachtanalyse.
Naast de "afstootkrachten" Fn en Fr heersen er nog talrijke wrijvingskrachten. de wrijvingsdruk, die door
wrijving aan o.a. de zuiger ontstaat, vermindert de heersende verbrandingsdruk en wordt als mechanisch
verlies aangeduidt. Dit wordt mechanische rendement η genoemd in de berekening voor het beschikbaar
vermogen van de motor. Voor het beschikbare draaimoment aan de krukas is de effectieve werkzame druk,
die uit de verbandingsdruk en wrijvingsdruk ontstaat, maatgevend. Vandaar de volgende formule die het
draaimoment uitdrukt in functie van de drukkracht aan de zuiger :
 

M = c x Fz x r

Het draaimoment staat dus in verhouding tot de drukkracht. Hoe groter deze kracht, hoe groter de druk.
Omdat F = p x A waarbij A de zuigeroppervlakte in m² en p de druk in Pascal (1bar = 100.000 Pascal)
krijgen we :
 

M = c x p x Az x r

Indien we c x p als effectieve werkzame druk pi samenvatten krijgen we :
 

M = pi x Az x r

De drukkracht is het grootst bij maximale cylindervulling. Dit ontstaat bij maximale opening van de gasklep.
Verder staat het draaimoment in verhouding tot de cylinderinhoud van de motor ofwel het volume V.
Hoe groter het volume, hoe meer daaimoment kan ontstaan.
 

M = K x pi x V

Hierbij is pi de effectief beschikbare druk in bar, V het volume (cylinderinhoud) van de motor in m³ en K een
constante die enkel voor deze formule geldt. Voor viertaktmotoren is K = 7,957981856.

Terugkerend naar de initiële krachtaanzet werd vastgesteld dat het draaimoment van de tangentiaalkracht Ft
afhangt. Deze varieert voortdurend tijdens de ladingswissel. Deze is bv negatief gedurende tijdens de
compressieslag, en dus ook het draaimoment. In deze fase wordt er geen vermogen afgegeven door de
motor. Er is arbeid noodzakelijk voor de verdichting van de gassen in de cylinder die uit de kinetische
energie van de draaiende motor-onderdelen wordt onttrokken.

Door verdichting ontstaat er maximale druk, onder bepaalde voorwaarden zoals de gaspedaalstand, en wordt
de zuiger naar onderen gedrukt. Hierdoor wordt Ft positief en neemt het draaimoment toe. Het maximale
draaimoment is beschikbaar als de zuiger kort voor het onderste dode punt aankomt.
Het door de motor afgegeven draaimoment correspondeert met het gemiddelde van de tangentiaalkracht.
Het is precies dit draaimoment of koppel dat men terugvindt in alle vermogensdiagrammen van een auto.
 

VERMOGENDIAGRAM VAN EEN BMW 760 / E65 / V12 - MOTOR

Bij het bestuderen van dit vermogendiagram valt het op dat zowel het koppel als het vermogen van het
toerental afhankelijk is. Het vermogen wordt groter naarmate het toerental stijgt. Deze staan in relatie
omdat bij iedere arbeidsslag van een zuiger een bepaald koppel of arbeid aan de krukas wordt opgebouwd.
Hoe meer zuigerbewegingen in een bepaalde tijd gebeuren, hoe meer arbeid er verricht wordt en hoe hoger
het vermogen wordt. Een hogere frequentie van de arbeidsslagen wordt door een hoger toerental bereikt.

Hieruit volgt dat vermogen, naast het toerental, in verhouding staat met het koppel, en dus in relatie
is met de druk en de cylinderinhoud.. Er is dus een relatie tussen het vermogen en het koppel.
 

P = φ x M x n

P = effectief beschikbare vermogen in kW φ = constante M = koppel aan de krukas in Nm n = toerental in t/min

Deze formule zal hier verder mathematisch bepaalt worden om haar correctheid en afhankelijkheid van de
fysische en wiskundige wetten te bewijzen. Tevens zal de factor φ worden bepaalt.
Het vermogen is fysich definieerbaar zoals hierboven beschreven. Vermogen is het quotient uit arbeid en tijd,
of het produkt van kracht en snelheid. Bovendien is voor het effectieve vermogen het toerental bepalend.
De krachtweg wordt beschreven in een baan en de snelheid v stelt de omtreksnelheid voor.
 

v =	π x d x n        60	d = diameter in meter (d = 2 x r) n = toerental in t/min 60 voor de omzetting van minuten naar seconden π = 3.1415...
Omdat P = F x v geldt ook P = π x 2 x r x n x F  =  M x n x π  =  M x n      (π / 30000 = 1 / 9550)                                                     60 x 1000             30000            9550

Nu is tevens de factor φ nu bepaalt en is 1/9550 of 0,0001047. Het getal 1000 in de noemer is voor de
omzetting van Watt naar Kilowatt.
Uiteindelijk hebben we de formule die het verband tussen vermogen en koppel aantoont :
 

P =	M x n  9550

Hier is duidelijk te zien dat het vermogen duidelijk van het koppel afhangt. Dit betekent dat het vermogen
niet veel over het ware karakter van de motor vertelt. Hiermee wordt een algemeen, doch verkeerd beeld, ontkracht. De meeste mensen beoordelen auto's en motoren naar hun vermogensweergave en denken, hoe hoger, hoe beter. Dit is niet helemaal verkeert, maar slechts half juist. Het vermogen is het resultaat uit 2 meetbare variabelen en moet dus "relatief" bekenen worden.

Om een motor, en dus een wagen, te beoordelen naar zijn dynamiek, rijgenot en "het optrekken"
is het koppel het best geschikt hiervoor.

Een voorbeeld zal dit verduidelijken. Een vrachtwagen en een Formule-1 hebben met 850 pk hetzelfde
vermogen. Hierbij ontwikkelt de vrachtwagen dit vermogen bij 1500 t/min en de F-1 slechts bij 15.000 t/min.
Zoals men ziet zijn dit 2 verschillende concepten met met zelfde vermogen maar verschillende koppel
en toerentalweergave. Terwijl de vrachtwagen reeds bij lage toerentallen op maximaal vermogen en snelheid
zit, zal de F-1 maximaal moeten versnellen, dynamisch en beweeglijk zijn vanwege het beperkte koppel
en het hogere toerental. (zie lager de grafiek)

Met de laatste formule wordt dus het effectieve vermogen bepaald die gemeten kan worden aan de krukas,
of beter aan het vliegwiel of koppeling. Deze indicatie van het vermogen van een bepaalde wagen vindt men terug in het gelijkvormigheidsattest dat door de constructeur wordt opgegeven. Deze waarde houdt reeds
rekening met alle wrijvingsinvloeden die ontstaan in het motordrijfwerk en is lager dan het inwendig vermogen
dat aan de arbeidscylinder ontstaat. Hoe dit vermogen berekent wordt volgt in onderstaande uiteenzetting.

Zoals eerder reeds vermeld geldt P = F x v of P = F x Δs/Δt. In de arbeidscylinder stelt de kracht een drukkracht voor zodat F = pi x Az, waarbij  A de zuigeroppervlakte in m² en pi de gemiddelde arbeidsdruk
of beter de gemiddelde geïndiceerde zuigerdruk voorstelt. Hierdoor krijgt men volgende formule :
 

Pi =

A x s x pi x z x n         60 x 2

z = aantal cylinders Δs = zuigerslag in meter (afstand van BDP tot ODP) Δt = arbeidstakt Omdat bij een viertakt slechts elke 2e slag wordt ontstoken geldt n/2. De factor 60 dient om het toerental in t/minuut om te zetten naar seconden.

Pi wordt uitgedrukt in daNm/s = 0,01 kW. Het produkt van A, s en z is gelijk aan de cylinderinhoud V in liter.
 

Het geïndiceerde vermogen is dus :

Pi =

pi x V x n      1200

in Watt

Uit deze formule kunnen we de mogelijkheden voor de vermogentoename bekijken.
  > De effectieve druk verhogen. Hoe hoger, hoe beter.
  > De cylinderinhoud vergroten. Hierdoor stijgt het koppel, maar ook de wrijving en de hitte.
  > Het toerental verhogen. Hierdoor stijgt het koppel, maar ook de wrijving en de hitte.

Het effectiefste en meest werkingsvolle is dat alle mogelijkheden bij serieproduktie van wagens wordt benut.
In bepaalde gevallen is dit anders zoals in de Formule-1 waarbij het reglement de grootte van de motor
bepaald. Ontwikkelaars moeten zich dus op het toerental concentreren. Deze kunnen tot 19.000 t/min gaan.
 

VERMOGENDIAGRAM VAN EEN FERRARI F-1 MOTOR

Typisch hierbij zijn het hoge toerental. Het koppel is begrenst op basis van de grootte van de motor.

Naast hoger vermelde varianten heeft men nog de mogelijkheid om vemogen te vermeerderen door verbetering
van de thermische en mechanische rendementen van het verliesvermogen.
het effectieve rendement η is gelijk aan het quotiënt Pe / Pi =  We / Wb. Hiermee wordt de verhouding van
het effectief vermogen tot het geïndiceerde vermogen gelijk aan de aan het vliegwiel beschikbare arbeid We
tot het door de brandstof aangevoerde arbeidsvermogen Wb. Hoe hoger het rendement, ideaal is 1,
hoe beter en produktiever is de motor en des te minder energie wordt er verloren door wrijving en warmte.

Er bestaan talrijke systemen, buiten het motorwerk, die bijdragen tot een vermogentoename zoals andere brandstofmengsels of geöptimaliseerde inspuitsystemen. Een zeer belangrijke en effectieve mogelijkheid is
de ladingdruk. Dit wordt uitvoerig beschreven in een verder artikel.  >> Lees verder op DRUKVULLING >>

Nu we de mogelijkheden voor een vermogenstoename bekeken hebben, bepalen we kort de afhankelijkheid
van het vermogen en het koppel tot het toerental.
 

P =

M x n  9550

of ook

M =

P x 9550      n

Er is reeds vastgesteld dat des te hoger het beschikbare vermogen is, des te hoger het toerental moet zijn
bij een onveranderde krachtontwikkeling. Voor het koppel geldt net het omgekeerde. Er is een omgekeerde
verhouding die stelt dat het koppel toeneemt bij lagere toerentallen. Ontwikkeld de motor bij een dubbel
toerental hetzelfde koppel resulteert dit een verdubbeling van het vermogen.

Dit maakt nogmaals duidelijk dat het maximale vermogen slechts bij hoge toerentallen aanwezig
is, terwijl het maximale koppel bij lagere toerentallen beschikbaar is.

De maximale waarden voor het vermogen en het koppel zijn in de vermogensdiagramma te herkennen aan
de maxima (top) van de betreffende grafieken. Terwijl het maximum van het koppel bij geringe toerentallen
herkenbaar is staat het maximale vermogen pas kort voor het maximale toerental ter beschikking. Hierbij
zijn beide bij een bepaald toerental écht beschikbaar, het zogenaamde nominale toerental. Bij dit toerental,
dat bij het maximale koppel bereikt wordt, is de verbrandingsdruk het grootst.
Gaswissel, mengselvoorbereiding en verbranding zijn op dit punt als optimaal te bestempelen. Direct na dit
nominale toerental daalt het koppel en het vermogen. Dit komt door de constant wisselende krachten,
die in de motor werken, waaronder ook de met het toenemend toerental groter wordende wrijvingskrachten.
Tot een bepaald toerental, dat voor iedere motor anders is vanwege het concept, is een motor in staat om
steeds meer kracht te ontwikkelen en zo het vermogen snel te doen toenemen. Draait de motor over dit
toerental, dan worden de wrijvingskrachten, talrijke tegenkrachten en de rijweerstand zo groot dat ze een
verdere krachtontwikkeling onmogelijk maken.
Het koppel daalt omdat de hoge verbrandingsdruk, dat enkel in een klein toerentalinterval wordt geproduceerd,
afzwakt en gaswissel, mengselvoorbereiding en verbranding slechter worden. Toch gebeurt deze afzwakking
niet zo snel omdat in principe het draaimoment of koppel nooit snel toeneemt of afneemt. Zo kan het
vermogen bij toename van het toerental nog steeds toenemen. Bij een bepaald toerental, kort voor het
maximale toerental, komt ook dit aan het maximum en daalt hierna snel omdat verdere krachtontwikkeling
onmogelijk is. (Maximale waarden voor vermogen en koppel ontstaan enkel bij volledig geopende gasklep.
Dit maakt een maximale toevloed van brandstofmengsel mogelijk en dus een maximale drukkracht)

Ideaal is een snel toenemend en langdurig constant blijvend koppel. Kortom dat er in een bepaald toerentalinterval een constant blijvend maximaal koppel beschikbaar is. Dit wordt de laatste tijd steeds frequenter bestudeerd bij nieuwe automotoren. Dat is mogelijk door nieuwe technieken zoals variabele
klep-openingstijden en laaddrukregelingen. Hierdoor wordt een wagen krachtiger en dynamischer.
 

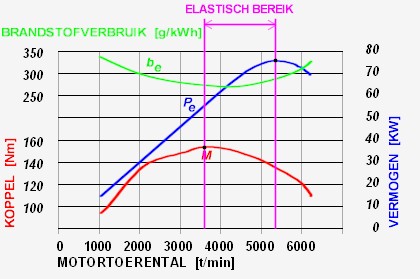
Zoals reeds vastgesteld treden de maxima van het koppel en vermogen nooit bij hetzelfde toerental op.
Vandaar dat het belangrijk is om een nieuw begrip te tonen, nl het elastisch bereik, dat het interval beschrijft
tussen het hoogste koppel en het hoogste vermogen. Deze is nooit gelijk aan nul omdat de beide maxima
nooit gelijktijdig optreden. Hoe kleiner echter dit interval wordt, hoe beter en werkingsvoller de rijprestatie
en dynamiek voor de automobilist is. Dit wordt bijvoorbeeld bereikt indien men het koppelmaximum over
een heel interval laat plaatsvinden.

Nu is duidelijk dat vermogen in verhouding tot het toerental het koppel weergeeft. In de voertuigtechniek
zijn verder nog twee andere verhoudingen gebruikelijk waarmee men de kwaliteit, efficiëntie en kracht van
een wagen mee kan beschrijven. Het eerste is het "cylinderinhoud-vermogen", of "liter-vermogen".
Dit beschrijft de verhouding het effectieve vermogen tot de cylinderinhoud in kW/L. Een motor wordt
meer geëvalueerd bij een hoger vermogen met een kleinere cylinderinhoud. Het tweede is het
"vermogengewicht" welke de verhouding beschrijft van de motormassa, of de complete wagenmassa tot het
effectieve vermogen. Dit beschrijft hoeveel KG per PK aanwezig zijn in kg/kW. Hoe minder gewicht een
KiloWatt "bewegen" moet, hoe beter en sterker een wagen is.

Samenvattend :

Het KOPPEL is de cruciale grootheid van een wagen als het om krachtontwikkeling gaat.
Het beschrijft hoeveel kracht aan de krukas wordt geproduceerd en hoeveel er bij overdracht
tot de weg tot beschikking staat.

Het VERMOGEN is eerder een relatieve waarde die resulteert uit het produkt van koppel,
toerental en een constante en daarmee weinig over het karakter van een motor vertelt.
Het vermogen geeft aan hoeveel arbeid aan de krukas per minuut wordt geproduceerd.